Problem 1.
Describe the motion of the simple pendulum.
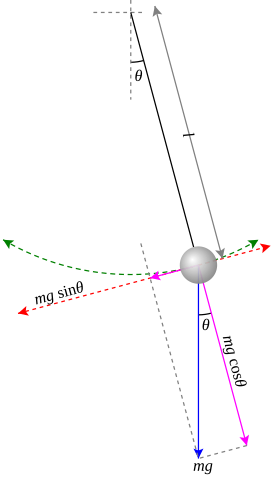
Fig.1. Simple Pendulum.
Newton's second law says \[ F=ma \] where $F$ is the sum of forces on the object, $m$ is mass, and $a$ is the acceleration. Because we are only concerned with changes in speed, and because the bob is forced to stay in a circular path, we apply Newton's equation to the tangential axis only. The short violet arrow represents the component of the gravitational force in the tangential axis, and trigonometry can be used to determine its magnitude. Thus, \begin{align*} F(t) &=-mg\sin(\theta(t))=ma(t),\\ a(t) &=-g\sin(\theta(t)), \end{align*} where $g$ is the acceleration due to gravity near the surface of the earth. The negative sign on the right hand side implies that $\theta$ and $a$ always point in opposite directions. This makes sense because when a pendulum swings further to the left, we would expect it to accelerate back toward the right.
This linear acceleration $a$ along the red axis can be related to the change in angle $\theta$ by the arc length formulas; $s$ is arc length in the following way
\begin{align*}
&\Step{1A}{s(t)=\ell\theta(t),}\\
&\Step{2A}{v(t)=s'(t)=\ell \theta\,'(t),} \\
&\Step{3A}{a(t)=s''(t)=\ell\theta\,''(t).} \\
\end{align*}
Thus we obtain \begin{equation} \label{eq:pendulumdiffeq} \bbox[lightblue,5px,border:2px solid red]{\color{#800000}{ \bf{\theta\,''(t)+\frac{g}{\ell}\sin(\theta(t))=0.}}} \end{equation} This differential equation is not easily solved, in fact, there is no solution that can be written in terms of elementary functions. However adding a restriction to the size of the oscillation's amplitude gives a form whose solution can be easily obtained. If it is assumed that the angle is much less than $1/10$ radian, that is, \[ |\theta|\lt\frac{1}{10}, \] then we can substitute $\sin(\theta)$ by $\theta$ (we recall that $\sin(x)=x+O(x^3)$). After that we obtain the equation of harmonic oscillator \[ \theta\,''(t)+\frac{g}{\ell}\theta(t)=0. \] Adding the initial conditions \[ \theta(0):=\theta_0\quad\text{and}\quad\theta\,'(0):=0 \] we can find the solution by standard method.
Let $\theta(t):=e^{\lambda t}$. Then substituting and simplifying we have the equation \[ \lambda^2+\frac{g}{\ell}=0. \] Its solutions are \[ \lambda_{1,2}=\pm i\sqrt{\frac{g}{\ell}}. \] Applying the Euler's formula ($e^{it}=\cos(t)+i\sin(t),\,t\in\mathbf{R}$) we arrive at the general solutions \[ \theta(t)=c_1\cos\left(\sqrt{\frac{g}{\ell}}t \right)+c_2\sin\left(\sqrt{\frac{g}{\ell}}t \right), \] where $c_1,c_2\in\mathbf{R}$ are arbitrary numbers.
To determine them we use the initial conditions. From $\theta(0)=\theta_0$ it follows \[ c_1=\theta_0. \] From $\theta\,'(0)=0$ it follows \[ c_2=0. \] So the solution of the initial problem is \[ \theta(t)=\theta_0\cos\left(\sqrt{\frac{g}{\ell}}t \right). \] The period of motion \[ T_0=2\pi\sqrt{\frac{\ell}{g}} \] is independent of the mass of bob.